In machine learning, normalization/standardization involves feature scaling, where the features (variables) used for making predictions are scaled to the same range of values. The feature scaling process is applied in the data preprocessing step before applying any machine learning algorithm.
Some of the machine learning algorithms e.g clustering, neural networks, are sensitive to the scale of the input variables, which makes the step of feature scaling necessary. Gradient based optimization methods, for instance, converge slowly when the features greatly differ in scale and have non-zero means. There can be different ways of scaling the variables like min-max normalization, variance scaling (standardization), L1 normalization, L2 normalization.
- Min-max normalization: transforms the data points to belong to a certain range, typically from 0 to 1;
- Standardization: subtract mean from each data point and divide by standard deviation;
- L1 normalization: divide each data point by the sum of all the values;
- L2 normalization: divide each data point by the square root of the sum of all the squared values;
Here we will focus on variance scaling, often simply referred to as normalization.
How do we standardize (variance scaling) the data?
z = (x - µ)/?
- Find mean and standard deviation for each feature;
- Subtract mean (µ) from the samples (x);
- Divide with standard deviation (?);
A common mistake in data science is performing standardization before the dataset split, i.e. evaluating the mean and the standard deviation based on both the training and the test data. It compromises the training procedure by introducing information on the test data in the form of the mean and standard deviation vectors computed based on the whole dataset, often leading to overly optimistic results during evaluation. Therefore, the standard practice is to split the dataset first and perform the standardization during both the training and scoring phase based on the training set alone.
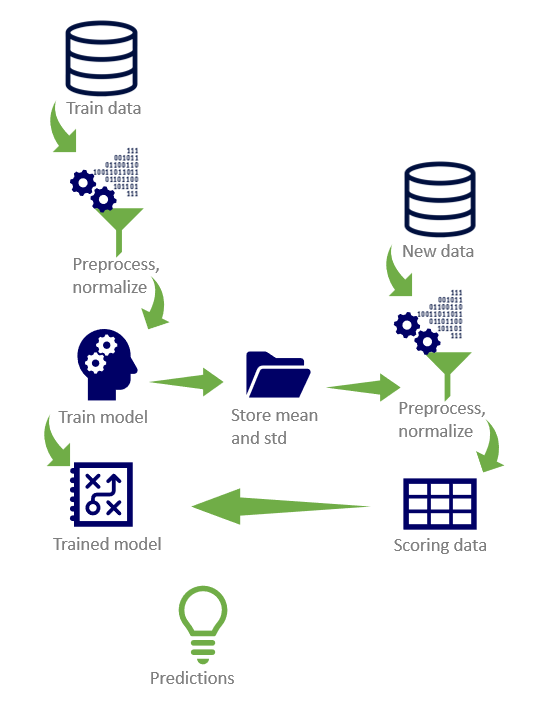
How do we standardize the data during real-time prediction making?
Updating the mean and the standard deviation vectors with novel data every time when generating predictions in a real-time setting with a deployed model can be quite unwieldly. What happens if the predictions have to be made in real-time and we have a large amount of historical data? In this case, loading all the historical data previously used for training is a very time consuming process. Another problem is the memory overhead associated with loading such a large amount of data, which requires spending more money for builiding a suitible setup that allows scaling up of the resources.
Therefore, to allow the predictive tool to run in real-time and to be cost efficient, only the new data available for scoring should be loaded each time. Besides being often unfeasible and expensive, the online update of the mean and the standard deviation is unnecessary if the model is updated and retrained frequently enough. In that case, it is safe to assume that the distribution of the total accumulated data does not vary substantially with the addition of novel data, and the update of the mean and standard deviation vectors can be limited to the times when the model itself is updated and retrained. Therefore, when using the deployed model to generate predictions during its operational lifetime, the previously stored mean and standard deviation of the historical (training) data are used to standardize the test data as well. During its operational lifetime, the model can be periodically retrained after encountering sufficient novel data and the normalization vectors can be updated based on the joint historical and novel data.
What are the elements of a predictive pipeline?
All the historical data available is used to train a predictive model, but before training the data has to be preprocessed and standardized. The newly available data on which the predictions have to be made also has to be preprocessed and normalized in the same way as the training data. Therefore, every time the model is trained or retrained, the mean and the standard deviation for each of the features are stored, such that they can later be used for standardization of the scoring data. After the preprocessing and standardization step, the data is ready to be scored with the previously trained model.